Home

Services

About Us

Projects

Contact Us

Disclaimer

Example: A one compartment vascular model for drug concentration

Please allow scripts to run on this page to format the mathematical notation.

The differential equation for the one compartment model of drug metabolism is $\frac{dC}{dt} = -kC(t)$, with $k>0$ and the initial condition $C(0) = C_0$.

	The simple exponential decay model for drug concentration over time from an initial dose of one unit of a drug.
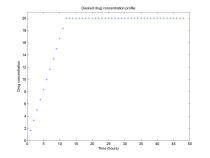	The desired drug input profile. This profile achieves a vascular drug concentration of 20 units over a 12 hour time period, maintaining the 20 unit concentration for the next 36 hours, after which the drug input is stopped.
	The computed drug input profile with the desired profile over a 72 hour time period. The computed profile matches the desired profile over the first 48 hours, after which the drug input was halted and the vascular drug concentration decreases.
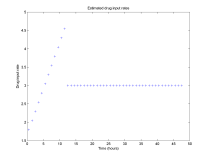	The constant drug input rates for each one hour time interval over the 48 hour time period for the desired profile.
	The drug concentration deviations for the computed profile relative to the desired drug profile. The deviations were computed as the desired profile minus the computed profile. The deviations observed for the computed profile during the first 12 hours are due to the nonlinearity of the exponential decay and the relatively steep slope of the drug input profile. A shallower slope and a longer ramp-up period for the drug concentration would reduce these deviations.