Home

Services

About Us

Projects

Contact Us

Disclaimer

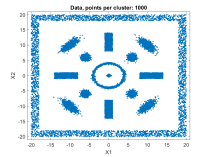
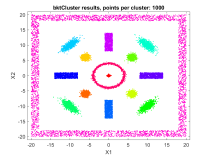
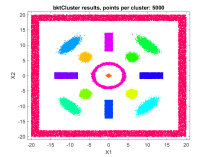
A fast automatic clustering algorithm for large data sets

A fast automatic algorithm for clustering large data sets in two or more dimensions has been developed: bktCluster. The algorithm can identify arbitrary cluster shapes and is robust in the presence of noise. The "automatic" aspect of the algorithm means that no configuration parameters may be needed to perform clustering on many data sets. The algorithm was designed with large data sets in mind, and it has a very aggressive large sample configuration as its default mode of operation, so for small or sparse data sets some parameter tuning may be desirable. The algorithm is parallelizable and is also suitable for distributed computing in a map-reduce type framework.

The algorithm and its underlying data structures also naturally lead to a fast classification algorithm for compatible new data, that is, data having the same distributional assumptions and characteristics as a data set that has previously been clustered using the algorithm.

Recognizing that no clustering algorithm is perfect and works well on all data sets of any size and spatial composition, the bktCluster algorithm also has a variety of parameters that can be modified to improve clustering performance for small data sets, noisy data sets, data sets with uneven cluster densities, and a variety of other real world situations.

Two types of simulated data sets were used to test the bktCluster algorithm. The first type of test data set consists of 15 clusters with varying shapes, orientations, and densities. The second type of test data set consists of 200 randomly generated 5 dimensional clusters, each normally distributed with randomly generated covariance matrices.

The first data set consisted of 15 clusters of various shapes, including concentric rings, round normal distributions, elongated and rotated normal distributions, rectangular uniform distributions, and an enclosing box where each segment was a rectangular uniform distribution and the cluster size was used for each of the segments with no overlap. For this test cluster sizes (N) of 100, 250, 500, 1000, 2500, 5000, 10000, 25000, 50000, and 100000 points were used to test the ability of the bktCluster algorithm to identify the clusters for a wide variety of sample sizes. Timing results for the different cluster sizes and a comparison to the MATLAB implementation of the DBSCAN algorithm are available below. The DBSCAN parameters used were an epsilon value of 2 and the square root of the total number of points as the minimum number of points per cluster.

N	Data	Clusters
1000
5000
Timings vs. DBSCAN	Timings for different sample sizes: bktCluster vs. DBSCAN

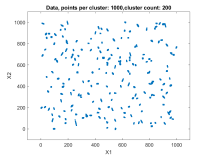
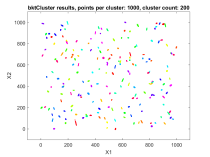
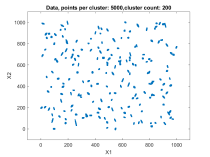
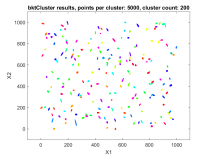
The second data set consisted of 200 normally distributed, 5-dimensional clusters with randomly generated centers and randomly generated covariance matrices. The centers were generated from a 5 dimensional uniform distribution in a hypercube with sides having a minimum value of zero and a maximum value of 1000. For this test cluster sizes (N) of 100, 250, 500, 1000, 2500, 5000, and 10000 points were used to test the ability of the bktCluster algorithm to identify the clusters for a wide variety of sample sizes. Timing results for the different cluster sizes and a comparison to the MATLAB implementations of the DBSCAN and k-means algorithms are available below. The DBSCAN parameters used were an epsilon value of 25 and the square root of the total number of points as the minimum number of points per cluster. For k-means the default settings were used with 1, 5, 10, 25, and 50 replications for each sample size. Results are presented for the first replication count achieving a match with the actual cluster centroids. The actual cluster centroids were computed using the data points assigned to each cluster. The figures show the first two dimensions of the data.

N	Data	Clusters
1000
5000
Timings vs. DBSCAN	Timings for different sample sizes: bktCluster vs. DBSCAN
Timings vs. k-means	Timings for different sample sizes: bktCluster vs. k-means